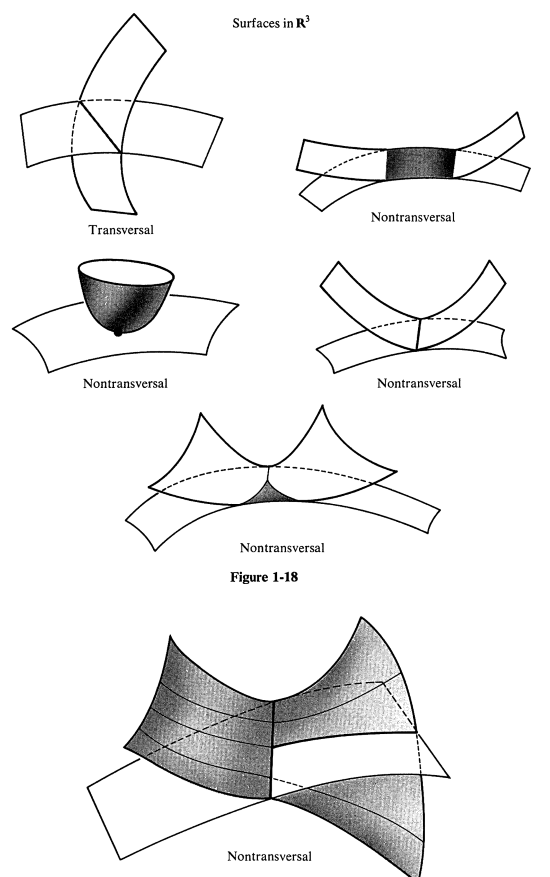
This is an introductory course in Differential Topology. The aim of this course is to introduce basic tools to study the topology and geometry of manifolds. We start with reviewing two key results from several variable calculus, namely the inverse function theorem and implicit function theorem which are essential to study differential manifolds. Throughout this course, we will discuss the theory of manifolds and a way to generalise differential, integral and vector calculus. By the end of the course, we should understand and able to work with manifolds, tangent and co-tangent bundles, transversality, Morse Lemma, Morse function, Whitney embedding theorem, Poincare – Hopf theorem, Sards theorem and its applications and many other things listed below in the course contents.